MoonChasing

Problem

Description

You are given a picture consisting of $nn$ rows and $m$ columns. Rows are numbered from $1$ to $n$ from the top to the bottom, columns are numbered from $1$ to $m$ from the left to the right. Each cell is painted either black or white.

You think that this picture is not interesting enough. You consider a picture to be interesting if there is at least one cross in it. A cross is represented by a pair of numbers $x$ and $y$ , where $1≤x≤n$ and $1≤y≤m$, such that all cells in row $x$ and all cells in column $y$ are painted black.

For examples, each of these pictures contain crosses:

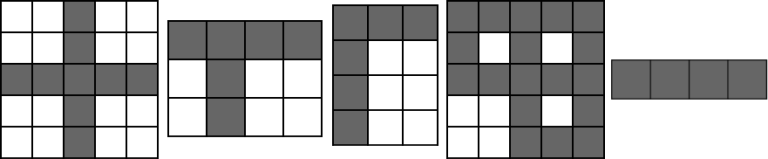
The fourth picture contains 4 crosses: at $(1,3)$ , (1,5)(1,5), $(3,3)$ and $(3,5)$ .

Following images don’t contain crosses:

You have a brush and a can of black paint, so you can make this picture interesting. Each minute you may choose a white cell and paint it black.

What is the minimum number of minutes you have to spend so the resulting picture contains at least one cross?

You are also asked to answer multiple independent queries.

Linux 内核源码果真精髓，相见恨晚。

offsetof 宏定义如下

1

#define offsetof(type, member) (size_t)&(((type*)0)->member)

container_of 宏定义如下

1
2
3

#define container_of(ptr, type, member) ({ \
     const typeof( ((type *)0)->member ) *__mptr = (ptr); \
     (type *)( (char *)__mptr - offsetof(type,member) );}) 

导论

1. 市场和市场营销定义

   从市场营销的角度看，市场就是商品交换关系的总和

   营销学中的市场：指的是具有特定的需求或欲望，而且愿意并能够通过交换来满足这种需要和欲望的全部潜在顾客。

   一般意义的市场：是商品交易的场所，是显在和潜在买主的结合体，是买卖关系的总和。

   营销是通过创造和交换产品及价值，从而使个人或组织满足欲望和需要的社会和管理过程。

   阅读全文 »

1. What is web container ?

   Web container is the component in J2EE which is responsible for handle request from client. Web Server application like tomcat is used to support basic service for web container, e.g., receive request and forward reply to client.

   阅读全文 »

• 全选

  普通模式下， gg 回到文件开始，v 进入可视模式， G 将光标移到文件结束。

• 复制到系统粘贴板

  这个首先要看 vim 是否支持系统粘贴板 vim --version | grep "clipboard" 我这里 clipboard 前是 + 号，表示支持。如果是 - 号，可以百度下方法。

  普通模式下，使用 "+y 复制到粘贴板。

• 交换相邻字符顺序

  我编程时有时因为输入太快而导致字符顺序错误。比如将 return 输入成 retrun, endl 输入成 ednl。这样子的话将光标移到出现错误的第一个字符。然后普通模式下 xp。

• 正常模式转到插入模式

  • i 当前光标前插入， I 当前行首
  • a 当前光标后插入， A 当前行尾
  • o 下一行插入， O 上一行插入

• D： d$

• ?：从下而上查找， / 自上而下查找

• 保存新文件：:w 路径+文件名

• :!+bash命令：运行终端命令

• :s/old/new：将旧的替换成新的，默认为当前行

• :3，5s/old/new：从第 3 行到第 5 行替换

• :s/old/new/g：全局替换

最近读《Effective C++》时读到了 new-handler 一章，了解了 new/delete 一些知识，才知道原来 new/delete 是可以个性化的。
先说简单的一个收获，C++ new 失败后默认后抛出异常，如果我们想让他失败时返回空指针，则应该使用如下写法。

1

int *pi = new (std::nothrow) int[100000000000L];

• 《一些好的开发习惯》：公众号自我介绍，科学上网助手、记录、虚拟机文件共享，链接：https://mp.weixin.qq.com/s/VNlzYchotgBbqiTn53jAsg
• 《校招面试前的一些准备》：春招找实习的准备工作（时间，简历，自我介绍模板，渠道，技术准备，深入部分、项目部分），链接：https://mp.weixin.qq.com/s/yXIY_-osPMAsySRFimktoQ
• 《掌握基础 - 方能决胜秋招》：技术类准备的基础工作，及一些资源的推荐，链接：https://mp.weixin.qq.com/s/zSQbfLv1YWR2oMvQwGXmug
• 《我的春招之路（上）》：谱哥春招经历，面经，链接：https://mp.weixin.qq.com/s/1Nu0v1iXPnb4p2ztXIKjiQ
• 《我的春招之路（下）》：面经，总结，链接：https://mp.weixin.qq.com/s/Cgu50L-MOeMwNBg-Sk_t9A
• 《腾讯百度实习经历》：链接：https://mp.weixin.qq.com/s/BaxJPkw7DunMvcJIibq_gA
• 《我的秋招准备》：Linux C/C++ 常见问题整理及 C++ 常见问题列表，链接：https://mp.weixin.qq.com/s/ClrX-JUTh4ftF4ZFSDgHnQ
• 《秋招玄学贴》：秋招经历、一些面经、注意事项，链接：https://mp.weixin.qq.com/s/wsBPWQiS6l3XX0jPQRnLvw
• 《我的秋招之路 (上)》：对于秋招的建议，面经，链接：https://mp.weixin.qq.com/s/8PeaTnAMbVU-kvMaye3SGw
• 《我的秋招之路 (下)》：面经，Linux C/C++ 一些题目，链接： https://mp.weixin.qq.com/s/r6bsLFzwvYnaBs5MrvXbRQ
  阅读全文 »

传送门：Circuit Board

Problem

Description

Arsh recently found an old rectangular circuit board that he would like to recycle. The circuit board has R rows and C columns of squares.

Each square of the circuit board has a thickness, measured in millimetres. The square in the r-th row and c-th column has thickness Vr,c. A circuit board is good if in each row, the difference between the thickest square and the least thick square is no greater than K.

Since the original circuit board might not be good, Arsh would like to find a good subcircuit board. A subcircuit board can be obtained by choosing an axis-aligned subrectangle from the original board and taking the squares in that subrectangle. Arsh would like your help in finding the number of squares in the largest good subrectangle of his original board.

Problem

传送门

Description

Bundle is an animal researcher and needs to go observe K dogs. She lives on a horizontal street marked at metre increments with consecutive numbers 0, 1, 2, 3 and so on. She begins in her home, which is at position 0. There are also N dogs on the street. The i-th dog is Pi metres to the right of her home on the street (multiple dogs can share the same position).

最近转移到了 Ubuntu 系统上，配了一波环境，逐步适应了些 Vim，虽然一开始觉得没有补全无所谓的，可以练练实力，再安装插件觉得麻烦，但后面还是觉得没有补全少点什么，于是决定还是下个 Vim 补全的插件。大约刻之前在赵老板博客上看到过一个关于 Vim 补全的插件赵老板博文链接，所以打算用那个，也就是 YouCompleteMe。据说这是 Vim 最难安装的插件？

安装步骤并不算麻烦吧：

1. 安装 Vundle （Vim 插件管理）
2. 用 Vundle 安装编译 YouCompleteMe
3. 配置 YouCompleteMe

前期工作

1. 确认你的 vim 版本在 7.3.584 以上。
2. 确认你的电脑支持 Python 2.x。
3. 需要 Vundle（vim 的插件管理工具）来管理你的插件。
4. 安装脚本需要使用 CMake。

以上几点大家如果没有配置好的话，网上有很多很详细的教程，这里就不细讲了。（完全照抄赵老板博客）