求逆序数对个数 (归并排序法)

发表于 更新于 分类于 ， 本文字数： 1.1k 阅读时长 ≈ 2 分钟

求逆序对数有多种方法，如归并排序法、线段树 \ 树状数组法、离散化。

归并排序法几乎就是归并排序。

白书讲解

markmark

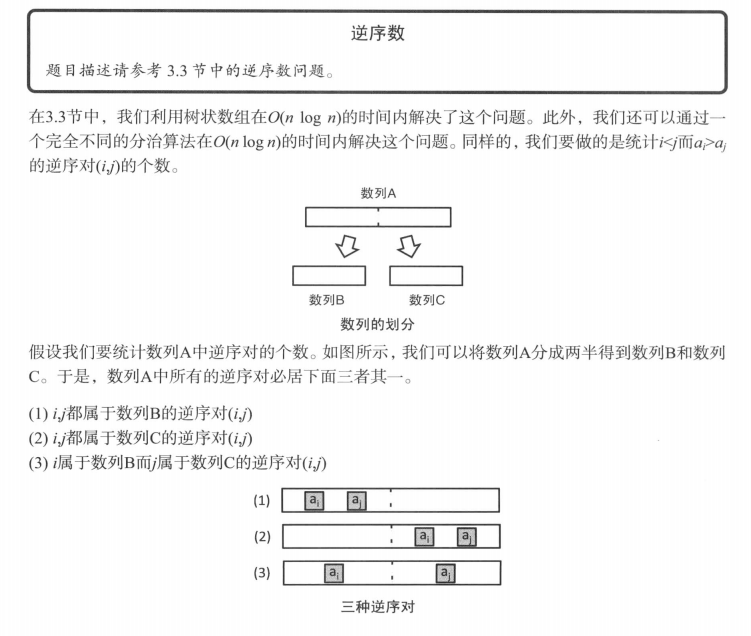
紫书代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
int A[MAXN]= {3, 6, 2, 1, 4, 5, 13, 7, 12, 10}, T[MAXN];

int merge_cnt(int l, int r) //统计区间为[l, r)
{
    int cnt = 0;

    if(r - l > 1)
    {
        int mid = l+r>>1;
        cnt += merge_cnt(l, mid);
        cnt += merge_cnt(mid, r);

        int p=l, q=mid, i=l;
        while(p<mid || q<r)
        {
            if(q>=r || (p<mid && A[p]<=A[q]))
            {
                T[i++] = A[p++];
            }
            else
            {
                T[i++] = A[q++];
                cnt += mid - p;
            }
        }

        for(i=l; i<r; i++)
            A[i] = T[i];
    }

    return cnt;

}

白书代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
int merge_count(vector<int> &a)
{
    int n = a.size();
    if(n<=1)
        return 0;

    int cnt = 0;
    vector<int> b(a.begin(), a.begin()+n/2);
    vector<int> c(a.begin()+n/2, a.end());

    cnt += merge_count(b);
    cnt += merge_count(c);

    int ai=0, bi=0, ci=0;
    while(ai < n)
    {
        if(bi < b.size() && (ci==c.size() || b[bi]<=c[ci]) )
        {
            a[ai++] = b[bi++];
        }
        else
        {
            cnt += n/2-bi;
            a[ai++] = c[ci++];
        }

    }

    return cnt;
}

一点建议

敲完数组实现的紫书代码和白书的 vector 实现的代码， 第一反应就是每次对 vector 的构造及初始化应该会费时间，于是测试了下。果不其然，在 $10^6$ 数据量下， 代码运行效果如图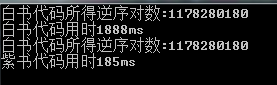：mark(突然发现当时复制的代码没改过来，第三行应为紫书代码，QAQ)

经过多次实验，用时稳定在本次用时左右。可以看出，用数组实现的效率远远高于 vector 实现。故推荐数组实现。